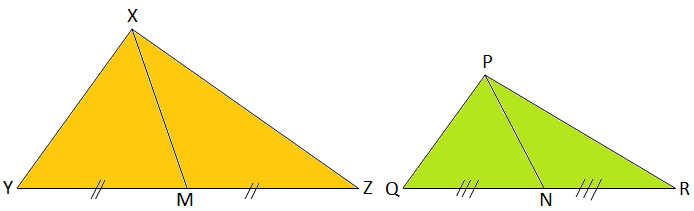
getyourfert.blogg.se - Similarity in right triangles

$similarity in right triangles$

#SIMILARITY IN RIGHT TRIANGLES HOW TO#

Let us understand these similar triangles theorems with their proofs.

SSS or Side-Side-Side Similarity Theorem.

$similarity in right triangles$

SAS or Side-Angle-Side Similarity Theorem.

AA (or AAA) or Angle-Angle Similarity Theorem.

There are three major types of similarity rules, as given below, These similar triangle theorems help us quickly find out whether two triangles are similar or not. We use these similarity criteria when we do not have the measure of all the sides of the triangle or measure of all the angles of the triangle. We can find out or prove whether two triangles are similar or not using the similarity theorems. The following image shows similar triangles, but we must notice that their sizes are different. Therefore, all equilateral triangles are examples of similar triangles. That means equiangular triangles are similar. Similar triangles are triangles for which the corresponding angle pairs are equal. So, if two triangles are similar, we show it as △QPR ∼ △XYZ Similar Triangles Examples We use the "∼" symbol to represent the similarity.

All corresponding sides of triangles are proportional.

All corresponding angle pairs of triangles are equal.

Similar triangles may have different individual lengths of the sides of triangles but their angles must be equal and their corresponding ratio of the length of the sides must be the same. Two triangles will be similar if the angles are equal ( corresponding angles) and sides are in the same ratio or proportion( corresponding sides).

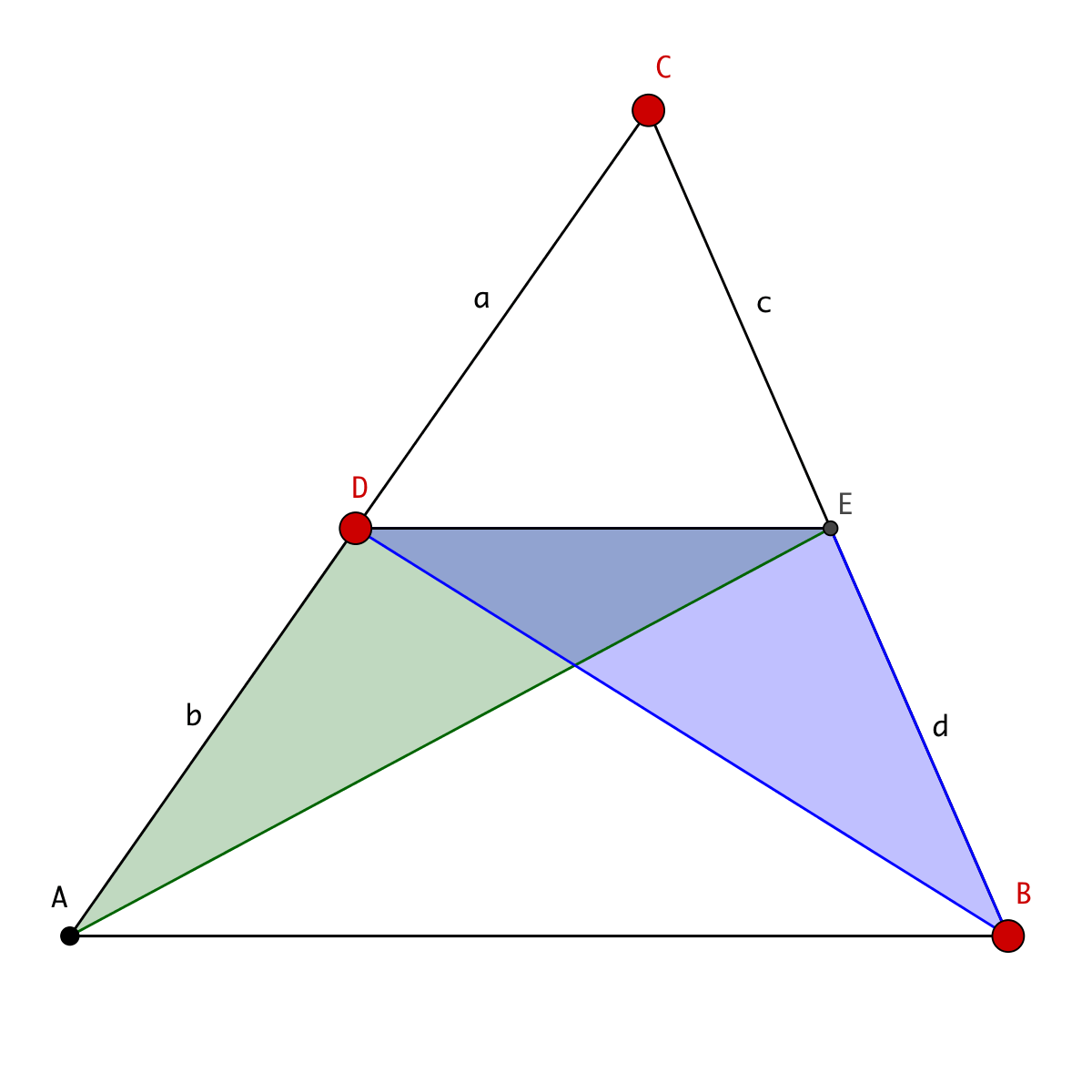
This property of similar shapes is referred to as " Similarity". That means similar shapes when magnified or demagnified superimpose each other. Two objects can be said similar if they have the same shape but might vary in size. Let triangle ABD and ECD be similar triangles.Īpply the Side-Angle-Side (SAS) rule, where A = 90 degrees.Similar triangles are the triangles that look similar to each other but their sizes might not be exactly the same. Let’s check if the proportions of the corresponding two sides of the triangles are equal.Ĭheck whether the two triangles shown below are similar and calculate the value k.īy Side-Angle-Side (SAS) rule, the two triangles are similar.ĭetermine the value of x in the following diagram. Given that the two triangles are similar, then Sum of interior angles in a triangle = 180°įind the value of x in the following triangles if, ΔWXY~ΔPOR.

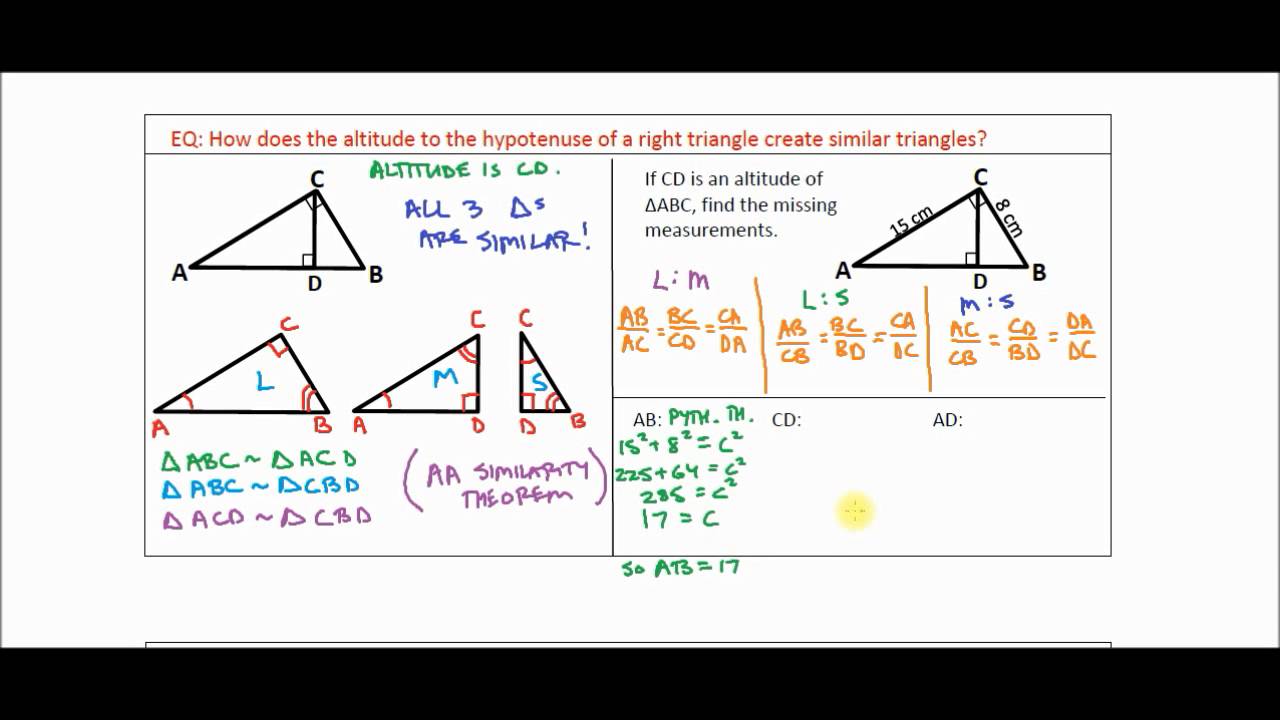
Let’s take a look at the following examples:Ĭheck whether the following triangles are similar There are two types of similar triangle problems these are problems that require you to prove whether a given set of triangles are similar and those that require you to calculate the missing angles and side lengths of similar triangles. Two triangles are similar if all the corresponding three sides of the given triangles are in the same proportion. The SAS rule states that two triangles are similar if the ratio of their corresponding two sides is equal and also, the angle formed by the two sides is equal. With the AA rule, two triangles are said to be similar if two angles in one particular triangle are equal to two angles of another triangle. There are three rules for checking similar triangles: AA rule, SAS rule, or SSS rule. These are postulates or the rules used to check for similar triangles. We can prove similarities in triangles by applying similar triangle theorems. The ratio of all the corresponding sides in similar triangles is consistent.Įach pair of corresponding angles are equal. The ratio of corresponding sides is congruent triangles is always equal to a constant number 1. Therefore, ΔABC ~ΔPQR~ΔXYZ Comparison between similar triangles and congruent triangles Features

The ratio of their corresponding sides is equal.ĪB/PQ = AC/PR= BC= QR, AB/XY= AC/XZ= BC/YZ.

Similar triangles are two or more triangles with the same shape, equal pair of corresponding angles, and the same ratio of the corresponding sides. The concept of similar triangles and congruent triangles are two different terms that are closely related.

#SIMILARITY IN RIGHT TRIANGLES HOW TO#

In this article, we will learn about similar triangles, features of similar triangles, how to use postulates and theorems to identify similar triangles, and lastly, how to solve similar triangle problems. Now that we are done with the congruent triangles, we can move on to another concept called similar triangles. Similar Triangles – Explanation & Examples